|
 |
| Plant Pathol J > Volume 38(3); 2022 > Article |
|
This article has been corrected. See "A Brief Guide to Statistical Analysis and Presentation for the Plant Pathology Journal" in Volume 38 on page 423.
Abstract
Statistical analysis of data is an integral part of research projects in all scientific disciplines including the plant pathology. Appropriate design, application and interpretation of statistical analysis are also, therefore, at the center of publishing and properly evaluating studies in plant pathology. A survey of research works published in the Plant Pathology Journal, however, cast doubt on high standard of statistical analysis required for scientific rigor and reproducibility in the journal. Here I first describe, based on the survey of published works, what mistakes are commonly made and what components are often lacking during statistical analysis and interpretation of its results. Next, I provide possible remedies and suggestions to help guide researchers in preparing manuscript and reviewers in evaluating manuscripts submitted to the Plant Pathology Journal. This is not aiming at delineating technical and practical details of particular statistical methods or approaches.
Measuring changes in subjects under observation and collecting data through replication are at the heart of experimental sciences. Plant pathology is not an exception to this. After collecting the data by measuring such changes, I get statistic to help us determine whether the difference between the two measurements is large enough to attribute to anything but chance. The difference is declared statistically significant, only if it is considered large by a criterion called P-value, which is obtained from performing a statistical test. Such streamlined practice provides a clear-cut yes or no decision on whether the results can be published or not, and is considered as a standard procedure.
However, I have been facing the reality of reproducibility crisis as suggested in a survey conducted by the journal ‘Nature’ (Baker, 2016). Despite the arguments that the reproducibility issue is not distorting the majority of the literatures, the reproducibility issue and its remedies definitely need our attention (Fanelli, 2018). If I define the reproducibility as the ability of independent researchers to obtain the same or similar results when repeating an experiment or test, the lack of reproducibility is not only a scientific issue, but also could be an ethical one (Resnik and Shamoo, 2017). Although there are many factors including pressure to publish (thus selective reporting of the data) and a growing burden of bureaucracy that cause and contribute to such reproducibility issues (Anonymous, 2016; Resnik and Shamoo, 2017), it cannot be emphasized enough that robust design of an experiment, correct application and interpretation of hypothesis test, and clear communication of the results are at the forefront of ensuring the reproducibility of scientific researches.
During the handling of the many papers published in the Plant Pathology Journal, I came across appreciable number of the manuscripts that could be improved in terms of study design, statistical analysis, and visualization of experimental data and results. Here I first provide the survey of the published papers in the Plant Pathology Journal for how basic and fundamental statistical concepts and techniques were used, and how results were visualized, explained and interpreted. Based on this survey, then I propose conceptual and practical guidelines that can be followed in preparation of manuscript to be submitted to the journal. I also provide the resources and further readings wherever appropriate for those who want to delve into the individual topics.
In order to systematically identify common mistakes and practices needing improvement, I have taken the survey of all the papers published between 2018 and 2019 (a total of 129 papers) (Supplementary Table 1: note that the papers information was provided without the author information, and individual papers randomly assigned to the arbitrary identification number), and grouped them into four categories. It should be noted that I did not include in our analysis the mistakes and misuse of statistics that are not frequently made. This survey showed that the followings are common: (1) unclear use of error bars in the bar graphs, (2) explanation and interpretation of P-values from statistical test, (3) likely use of pseudo-replication, and (4) lack of clarity in explaining experimental set-up pertaining to how replicates were made and statistical test was performed (Fig. 1).
Among eighty papers in which error bars are used to show the variation within the data, about 29% of them did not clearly specify whether the error bars indicate standard deviations or standard errors (Fig. 1A). A 7.5% of them did not provide any explanation at all. Out of 79 papers that have run statistical tests at least once, the resulting p-values were specified only in 21.5% of them (Fig. 1B). Approximately the two third of papers (63.3%) indicated P-values as ranges (for example, P < 0.05 or P < 0.01). Although use of such notation is a common practice, I suggest that specifying exact P-value is a much better practice. The survey also revealed that some studies appear to run their statistical test based on pseudo-replicated data set (Fig. 1C). Pseudo-replication occurs when counting the replicates (or observations) that are not independent on each other as independent ones and include them all in statistical testing, incorrectly inflating the sample size. However, it was difficult to know the use of pseudo-replication with great certainty due to the lack of clear description about experimental set-up in more than a half of papers examined (Fig. 1D). Many papers stated that three or more replicates were used, but it was not clear whether distinction between biological and technical replicates were made in choosing the data sets for their statistical tests.
The survey period spans only two years. Despite the limitation, it is not unreasonable to extrapolate the survey results to assume that examples of these errors and mistakes abound in other years of publications. From the next section on, I clarify a few basic concepts in statistics that I think would help remedy the problems I have encountered and improve reproducibility of the work.
Let’s start with the concept of statistic. A statistic refers to the quantities obtained (or rather correctly computed) from values in a sample. A statistic is used in a variety of purpose. For example, it can be used either to summarize the sample data (descriptive statistic) or to infer population parameters such as population mean that cannot be directly measured and so are usually unknown (inferential statistic). There is often confusion between standard deviation (SD) and standard error (SE). However, SD is a descriptive statistic, whereas SE is an inferential statistic. The SD describes how much dispersion or variability there is within your single sample. It may be used to show accuracy of your measurement or experiment, as a low SD indicates close clustering of your data around the sample mean. In contrast, SE describes variability across the multiple samples of a population. It therefore tells us how accurately our sample reflects the whole population. Since I usually have a single sample, however, SE should be estimated from a single sample in our hand. A SE decreases as sample size (i.e., number of values in the sample) increases, indicating that the larger your sample is, more precise your estimation about the population is. Unlike SD, SE is useful in hypothesis testing, since it helps judge how representative your sample is when drawing any conclusion about the actual population that you are interested in.
I propose that the authors should be aware of such distinction between SD and SE, and use them accordingly. This includes making a clear indication in the manuscript about use of either SD and SE, so that the reviewers and readers would be able to better evaluate the data presented in the manuscript.
As explained briefly in the previous section, pseudo-replication refers to taking the incorrect level of replication. I suspect that such pseudo-replication often comes from not distinguishing biological replicates from technical replicates (Bell, 2016; Vaux et al., 2012) To illustrate the problem of pseudo-replication and how pseudo-replication might occur, I ran a computer simulation, assuming a hypothetical situation where a researcher is measuring and comparing between control and treatment samples (R code for the simulation and production of graphs is available as Supplementary Material 1). Please note that outcome may vary whenever the code is run as the values are randomly generated anew. True mean values of control and treatment population, which are not known in most cases and have to be inferred from the sample, were set to be 8 and 6, respectively. Three values were randomly taken three times from normal distributions having mean values of 8 and 6, respectively, in order to simulate the situation in which three independent experiments (biological replicates) were conducted with three technical replicates (repeats) (Fig. 2). To emulate experiment-to-experiment variations, standard deviations of normal distribution were set to be different among the biological replicates. Although each set of measurements (sample) was drawn from the normal distributions having the same mean values, sample means for individual biological replicates differ from the true means owing to the small sample size (n = 3) and varying standard deviations (Fig. 2A).
With this dataset given to the researcher, the following three scenarios are possible in running a statistical analysis (in this case, t-test) and reporting P-value. First, the researcher runs t-test for each biological replicate (n = 3), comparing the control and treatment groups, and finds that all three P-values are below 0.05. This seems to suggest to the researcher that there is a statistically significant difference between the control and treatment groups, and that his or her finding is reproducible. Accordingly, the researcher decides to report the means, standard errors, and P-value obtained from the first biological replicate only (panel 1 in Fig. 2A and B). Alternatively, the researcher may decide to aggregate all the data points across three biological replicates (n = 9) and run a t-test using them. This would usually result in much smaller P-values (more significant!) despite the smaller discrepancy between control and treatment mean values than the first scenario (compare Fig. 2B and C). Lastly, the researcher may want to take individual means of biological replicates (n = 3), and use them to run a t-test. This would lead to the larger P-value than the one obtained in the second scenario due to the smaller sample size. Now the question is what would be the correct practice to do?
In the first scenario, the researcher is presenting only a single set of data among the three sets, and thus reviewers and readers are oblivious of variability that exists in other biological replicates. Such is considered as selective reporting of data that should be avoided. The second scenario is the one where the concept of pseudo-replication matters. Including all the data points without discerning biological from technical replicates is artificially inflating number of samples (in statistical term, degree of freedom). Such pseudo-replication can lead to spurious results, leading to an incorrectly significant test. Use of pseudo-replication, therefore, call into question the validity of your experiment and analyses. I recommend the researchers to follow the third scenario in running statistical tests and reporting the results, although this is not perfect because when some of biological replicates have different number of technical replicates (unbalanced design of experiment), this would not be reflected in the mean values. Alternatively, the researcher may want to use statistical models such random effects model, in which the dependency among data points is accounted for. This enables the researcher to make use of all the data for the analysis. I am not going to go into the technical details of random effects model here, as it goes beyond the scope of this paper. However, I have included the code in the Supplementary Material 1 that runs a linear mixed model for the simulated data set, so that the results can be compared for those who wants to delve into the topic.
If you are comparing control and treatment groups, then you would probably use Student’s t-test to analyze the data. Null hypothesis of the t-test is that both groups have identical means. The t-test then calculate the probability of seeing the observed data, assuming the null hypothesis. This probability is the P-value. If P-values are below a certain threshold, then the null hypothesis is rejected and observed difference in mean values are declared ‘significant’, which is often denoted by an asterisk(s). This is the way that most of such so-called null hypothesis significance testing (NHST) are performed, regardless of types of statistical test employed. The P-value is certainly a useful method to summarize the study results and provide a basis for dichotomous decision. It should be noted that P-value, however, is not a measure of how right your hypothesis is, or how significant the difference is. Rather it is a measure of how unlikely the observed difference should be if there is no actual difference between the groups. So, P-value should not be considered as a measure of the size of the effect. There has been fierce debate about use of P-value and its influence on science (Goodman, 1999, 2001). Despite much debated problems of P-value, use of P-value is so widespread and prevalent that it is almost impossible to publish without it.
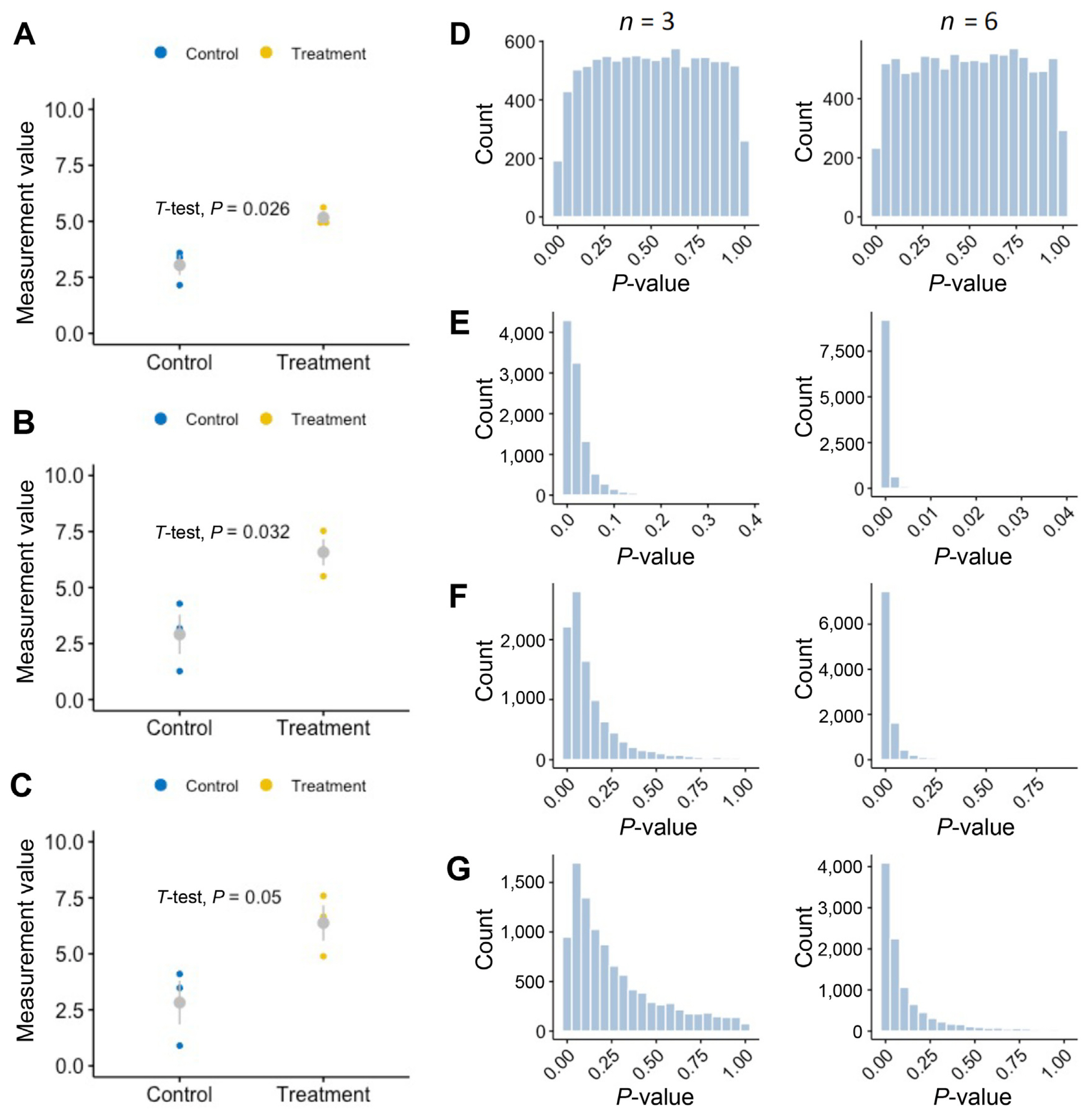
Here I are going to look into the situations in which use or misuse of P-value becomes problematic. One reason for problem with P-value is the arbitrary nature of its cutoff value. For demonstration purpose, I have generated again random datasets containing values that are randomly drawn from normal distribution having mean values of 3 and 5, respectively (Supplementary Material 1). When standard deviation is 0.5 (Fig. 3A), t-test gives us the P-value of 0.026, which is below the commonly used cutoff value of 0.05, supporting that the mean values of control and treatment groups are from different populations (please note again that you would end up obtaining a slightly different P-value whenever you run the code). As I increase the standard deviation to 1 and 2 (Fig. 3B and C, respectively), P-values from t-test increase up to 0.05. This clearly shows how use of arbitrary cutoff in determining statistical significance can be misleading. Decisions can be even more complicated when, for example, marginal P-values such as P = 0.048 and P = 0.052 were obtained. Is P-value of 0.048 significant, while P-value of 0.052 is not?
The second reason is that P-values are subject to experimental design and nature of experiment. To illustrate this point, I ran additional simulations (Fig. 3D-G). Fig. 3D shows that running t-test for two groups (control and treatment) of numbers randomly drawn from the identical normal distribution (mean = 3 and SD = 0.5) could result in declaration of significant difference (cutoff value of 0.05) between the two groups just by chance in approximately 5% of cases, regardless of sample size. In contrast, running t-test for two groups of numbers randomly drawn from different normal distributions (one with mean = 3 and SD = 0.5, and the other with mean = 5 and SD = 0.5) shows that P-value are larger than 0.05 in considerable number of tests when sample size is 3 (left panel). Increasing the sample size in this case makes sure that all the test ends up detecting difference between the two group (right panel). However, when variability (standard deviation of normal distribution) within samples increases (SD = 1 and 1.5 for Fig. 3F and G, respectively), t-test fails to detect the difference between the two groups, although this is mitigated by a larger sample size (right panels of Fig. 3F and G). These results show that P-values should be interpreted with great care in the context of experimental design (e.g., sample size) and nature of experiment (e.g., large variability inherent to the type of experiment). A statistically insignificant difference, therefore, does not mean there is no difference at all.
Last but not least reason is that P-value are not measures of effect size, so similar P-values do not always mean similar effects. Suppose that I see two groups that are different and the associated P-value support this conclusion (t-test). How meaningful then the P-value as low as 1 × 10−50 is in this case? It would be much easier to understand what this question really implies if I rephrase it as follows: is it more significant than 1 × 10−10, or conversely, is it less significant than 1 × 10−100? As mentioned above, P-value is not indication of effect size but just a measure of how unlikely your data is when assuming the null hypothesis. This suggests that our propensity to look for a difference in significance should be replaced by a check for the significance of the difference. I recommend readers to take a look at some of the efforts toward this shift from dichotomy based on P-value to more quantitative and Bayesian reasoning by visiting https://www.estimationstats.com/#/ (Ho et al., 2019) and https://www.sumsar.net/best_online/ (Kruschke, 2013).
Certainly, there is no single scientist who don’t agree to the importance of research reproducibility. However, I also know that there is so many barriers that I have to hurdle in order to achieve that. Here I tried to not only clarify some of the basic concepts but also provide cautions and remedies for issues raised by the survey of published results in the Plant Pathology Journal. In particular, I strongly recommend the followings: avoiding pseudo-replications, having as many biological replicates (not technical replicates) as possible, providing candid presentation of p-value and careful interpretation of it. I believe that being conscious about these issues and trying to avoid mistakes/errors are an important first step toward improving reproducibility and quality of the work published in the journal. Such efforts should be made by both authors of the manuscript and reviewers who would evaluate it. To that end, I provide a list of the recommended readings in order to help those who are eager to learn more (Altman and Bland, 2005; Diaba-Nuhoho and Amponsah-Offeh, 2021; Huber, 2019; Kass et al., 2016; Lazic, 2019; Madden et al., 2015; Nuzzo, 2014).
Electronic Supplementary Material
Supplementary materials are available at The Plant Pathology Journal website (http://www.ppjonline.org/).
Fig. 1
Survey results of the statistical analyses published in the Plant Pathology Journal during the year 2018 and 2019. Each pie chart summarizes result about one of the following: specification of error bars in the graphs (A), specification of P-values (whether or not P-value are provided as exact value or not) (B), possibility of pseudo-replication in statistical analysis (C), and how clearly the experimental design and statistical analysis were described (D). The percentages were given relative to the total number of papers (provided at the bottom right corner of each panel) in which the relevant information is available.

Fig. 2
Simulated dataset for demonstration of pseudo-replication. A dataset was generated by randomly drawing three numbers three times from normal distributions having different standard deviations (A). For control and treatment groups, the numbers were taken from normal distributions centered on 8 and 6, respectively. Each panel (from 1 to 3) represents different biological replicates, while color dots within panel indicate measurement values obtained from technical replicates. Black dots represent mean of three sample values. Three possible scenarios in which researchers can take to summarize and run a statistical test such as t-test are shown in graphs (B-D). A researcher may want to show the results of the first biological replicate only (B), or may want to aggregate all the data points across three replicates (C) leading to the pseudo-replication. Lastly, he or she may want to average the dependent data points (technical replicates in this case) and use three of them to make comparison between control and treatment groups (D).
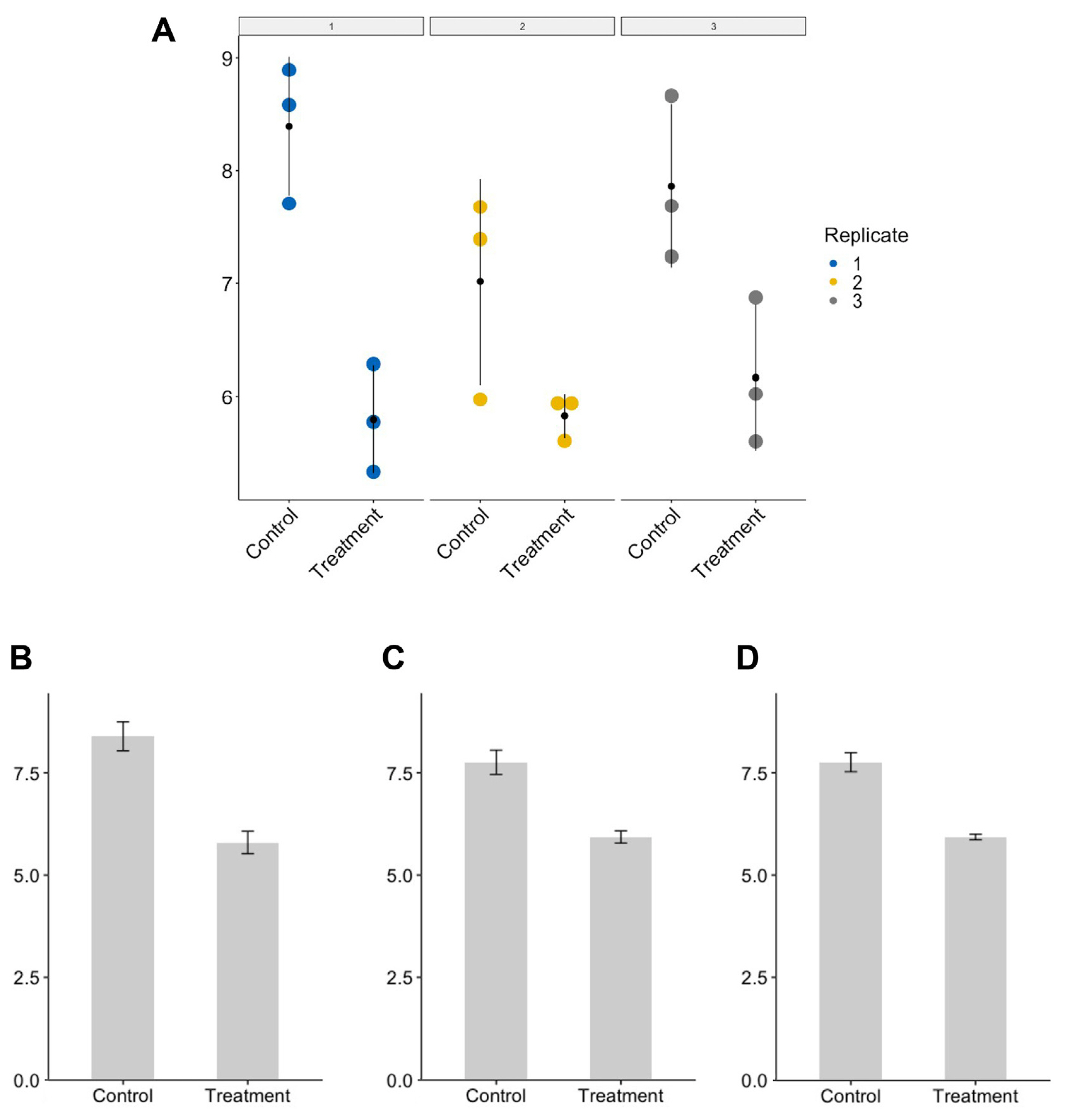
Fig. 3
Simulation of data sets for demonstration of issues associated with P-value. Effect of experimental variations on P-values was simulated by comparing control and treatment groups consisting of randomly drawn numbers from normal distributions centered on either 3 for control or 5 for treatment group (A-C). Standard deviations of normal distribution for panels A, B, and C were set at 0.5, 1, and 2, respectively. Effect of sample size and variation in combination on P-values were simulated by sampling the numbers and getting the P-values from t-test repeatedly (10,000 times) (D-G). Simulation results were summarized by histograms drawn based on P-values. The left and right panels represent the cases when sample size is 3 and 6. (D) The numbers were taken from the identical normal distribution for both control and treatment groups. (E-G) The number were drawn from normal distributions having mean values of 3 and 5 for control and treatment groups, respectively. Standard deviations of the normal distributions were set at 0.5, 1, and 2 for panels E, F, and G, respectively.
References
Diaba-Nuhoho, P. and Amponsah-Offeh, M. 2021. Reproducibility and research integrity: the role of scientists and institutions. BMC Res. Notes 14:451.



Fanelli, D. 2018. Opinion: is science really facing a reproducibility crisis, and do we need it to? Proc. Natl. Acad. Sci. U. S. A. 115:2628-2631.


Goodman, S. N. 1999. Toward evidence-based medical statistics. 1: the P value fallacy. Ann. Intern Med 130:995-1004.


Ho, J., Tumkaya, T., Aryal, S., Choi, H. and Claridge-Chang, A. 2019. Moving beyond P values: data analysis with estimation graphics. Nat. Methods 16:565-566.


Kass, R. E., Caffo, B. S., Davidian, M., Meng, X.-L., Yu, B. and Reid, N. 2016. Ten simple rules for effective statistical practice. PLoS Comput Biol. 12:e1004961.



Lazic, S. E. 2019 Genuine replication and pseudoreplication: what’s the difference? URL https://blogs.bmj.com/openscience/2019/09/16/genuine-replication-and-pseudoreplication-whats-the-difference/. 10 January 2022.
Madden, L. V., Shah, D. A. and Esker, PD. 2015. Does the P value have a future in plant pathology? Phytopathology 105:1400-1407.


- TOOLS
-
METRICS

-
- 1 Web of Science
- 0 Crossref
- 0 Scopus
- 3,496 View
- 283 Download
- ORCID iDs
-
Junhyun Jeon

https://orcid.org/0000-0002-0617-4007 - Related articles



 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC Download Citation
Download Citation Supplement1
Supplement1 Print
Print